《圆的标准方程》说课稿：一等奖背后的深度剖析

在数学的浩瀚星空中，圆以其独特的完美对称性和广泛的应用领域，成为解析几何中一颗璀璨的明珠，我将以“圆的标准方程”为切入点，深入探讨这一主题的说课内容，旨在揭示其教学价值，分享一等奖背后的成功经验。

一、课程地位与价值

承上启下的知识桥梁

圆的标准方程，作为高中数学解析几何的重要组成部分，不仅是对初中圆知识的深化与延伸，更是后续学习直线与圆的位置关系、圆锥曲线等复杂内容的基石，它巧妙地将代数与几何融为一体，通过方程的形式精确地刻画了圆这一几何图形，为学生提供了一种强有力的数学工具，用于解决更为广泛的几何问题。

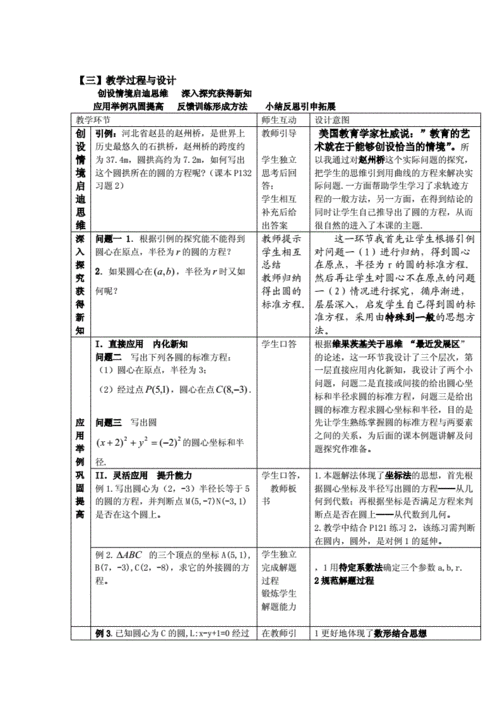
培养数学思维的沃土

学习圆的标准方程，不仅是为了掌握一种计算技巧或记住一个公式，更重要的是通过这一过程，培养学生的方程思想、等价转化思想以及数形结合的能力，这些思想是数学学习的灵魂，能够帮助学生在面对复杂问题时，迅速找到问题的关键，灵活运用已知条件，实现问题的高效解决。

二、教材内容剖析

标准方程的构建逻辑

圆的标准方程（\(x-a）^2 + （y-b）^2 = r^2\)（\(r\) 为半径且 \(r > 0\)），其推导过程体现了数学的逻辑美，从确定圆的几何要素——圆心坐标 \((a, b)\) 和半径 \(r\) 出发，利用两点间距离公式，我们可以建立起圆上任一点到圆心距离等于半径的等式，进而化简得到标准方程，这一过程不仅加深了学生对圆的几何性质的理解，也锻炼了他们的代数运算能力和逻辑推理能力。

教材例题的精心编排

教材中的例题设计，既注重基础知识的巩固，又兼顾了思维能力的提升，通过不同条件下圆的标准方程求解，让学生学会根据圆心坐标和半径快速写出方程，并能够从方程中提取出圆心和半径的信息，例题还涉及了利用圆的标准方程解决实际问题，如判断点与圆的位置关系、求圆的切线方程等，这些应用不仅增强了学生对知识的理解，也激发了他们探索数学世界的兴趣。

三、说课亮点：一等奖的启示

情境创设，激发兴趣

一等奖的说课往往始于一个引人入胜的实际情境，比如设计一个圆形喷泉的数学模型，要求学生根据喷泉的半径和中心位置建立圆的方程，这样的情境不仅贴近生活，还能迅速吸引学生的注意力，使他们意识到数学与现实世界的紧密联系，从而激发起强烈的学习欲望。

互动探究，促进理解

在教学过程中采用“问题－探究”模式，通过一系列环环相扣的问题引导学生主动思考、合作探究，先让学生回顾初中关于圆的定义和基本性质，然后提出如何在坐标平面内表示圆的问题，接着逐步引导学生通过画图、推导、验证等方式得出结论，这种教学模式不仅增强了学生的参与感和成就感，还促进了他们对知识的深刻理解。

技术融合，创新教学

一等奖的说课稿中常能见到现代信息技术手段的有效融入，比如利用多媒体展示圆的标准方程的动态演示，通过动画形式展现圆心、半径变化对方程的影响，或是模拟实际应用场景中的数学问题解决过程，这些直观、生动的教学资源不仅提高了课堂效率，也使得抽象的数学概念变得易于理解，极大地激发了学生的学习热情。

四、面临的挑战与应对策略

思维定势的挑战

学生在学习圆的标准方程时，可能会受限于已有的几何直觉和思维习惯，难以迅速适应用代数方法解决几何问题的新思路，对此，教师需要耐心引导，通过具体实例和类比法帮助学生打破思维定势，逐步建立起代数与几何之间的桥梁。

坐标法的熟练运用

坐标法是解析几何的核心，但在实际应用中，学生往往因为对坐标系的不熟悉或运算能力的不足而遇到困难，加强坐标法的基础训练，提高学生的代数运算能力和空间想象能力，是提高教学质量的关键，可以通过增加相关练习、开展小组合作学习等方式来实现这一目标。

《圆的标准方程》一节不仅是数学知识的传授，更是思维方法和数学素养的培养，通过精心设计的教学活动，我们不仅能让学生掌握圆的标准方程这一重要工具，更能激发他们对数学的热爱，为后续更复杂的学习奠定坚实的基础，一等奖的说课，正是对这一理念的最佳诠释，在未来的教学中，让我们继续探索、创新，为培养具有高度数学素养的人才贡献力量。